3541
3D Real-Time MRI of Vocal Tract Shaping1University of Southern California, Los Angeles, CA, United States
Synopsis
We demonstrate a new three-dimensional (3D) real-time MRI technique for the study of dynamic vocal tract shaping during human speech production. This, for the first time, enables a comprehensive assessment of vocal tract area function dynamics. We used a minimum-phase 3D slab excitation, stack-of-spirals gradient echo sequence, pseudo golden-angle view order in
Introduction
Real-time MRI (RT-MRI) has emerged as a powerful tool for speech production research due to its numerous advantages over alternative imaging and movement tracking modalities1–3. Speech scientists seek a comprehensive understanding of vocal tract dynamics and can utilize real-time imaging of the vocal tract to extract linguistically meaningful patterns in airway constrictions and area changes during speech. Current RT-MRI techniques, however, have been limited to one or a handful of 2D imaging planes4, or to 3D imaging with low temporal resolution5 or requiring multiple task repetitions6. To address the unmet need for 3D dynamic data on airway shaping during speech, we have developed a new 3D RT-MRI technique that achieves 2.4 x 2.4 x 5.8 mm3 spatial resolution and 72 ms temporal resolution over a 200 x 200 x 70 mm3 field-of-view (FOV), using parallel imaging and simple spatiotemporal constraints previously validated in the context of 2D RT-MRI.Methods
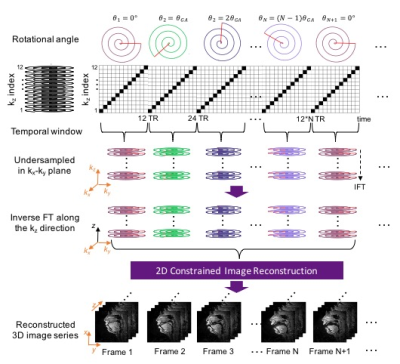
Pseudo Golden Angle Stack-of-Spiral Sampling Pattern
Figure 1 illustrates the data sampling scheme. A spiral pseudo-golden angle sampling pattern is used in the kx-ky plane and Cartesian sampling is employed along kz. Each spiral is acquired for all kz phase encodes (linear order) before moving to the next spiral, with a golden angle increment, . The spiral angle is reset after 34 interleaves4.
Experiments
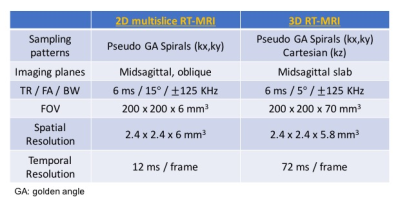
All experiments were performed on a 1.5T scanner (Signa Excite, GE Healthcare, Waukesha, WI) using a real-time interactive imaging platform (RT-Hawk, Heart Vista Inc, Los Altos, CA)7. A custom 8-channel upper-airway coil4 was used for signal reception. 3D slab excitation was achieved by using a minimum-phase RF pulse designed with the Shinnar-LeRoux RF design tool8. The pulse excited a mid-sagittal slab with 5cm thickness using a flip angle (FA) of 5° and TBW of 16. Data acquisition was performed using a golden angle stack-of-spirals gradient echo sequence. For comparison, we performed 2D pseudo golden angle RT-MRI with two interleaved slices — one midsagittal and one oblique slice — relevant to the speech task4.
All imaging parameters used are given in Table 1.
Image Reconstruction
We employed a sparse SENSE reconstruction with spatiotemporal finite difference constraints4 for both the 3D and 2D datasets. 3D reconstructions were performed slice-by-slice, by first inverse Fourier transforming data along the (fully sampled) kz direction. The same regularization parameters (= 0.02 and = 0.01) were used for 3D and 2D datasets. Reconstruction was performed using the Berkeley Advanced Reconstruction Toolbox (BART)9.
Measurement of Vocal Tract Area Function
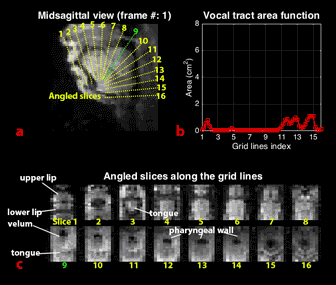
We obtained grid lines that were perpendicular to the airway centerline from a mid-sagittal plane10 and extracted angled slices along the grid lines through the 3D volume (61 slices, with 16 shown in Figure 4c). From each of angled slices, we estimated the vocal tract area function using a region growing method11, applied in this case to the dynamic data.
Results and Discussion
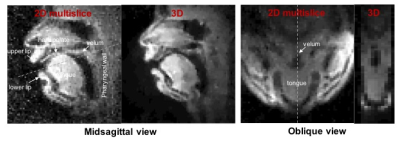
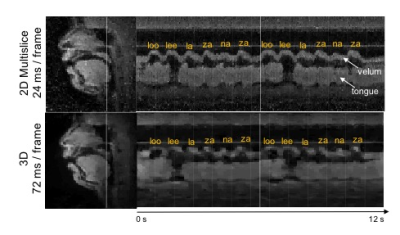
Figure 2 shows reconstructed images of the upper airway from 3D and 2D multislice RT-MRI taken from an acquisition in which the subject spoke the syllables /loo/-/lee/-/la/-/za/-/na/-/za/, repeated twice at a natural pace. Figure 3 shows 2D and 3D intensity vs. time profiles in the region of the vocal tract in which velum and tongue body movement occur. The 3D profile result provides adequate quality for speech scientists whom we have consulted to discern velum actions specific to nasal versus oral consonants and tongue body actions utilized for vocalic airway shaping.
Figure 4 (animated) shows vocal tract area function dynamics. Critical lingual constriction events are visible along the length of the vocal tract. Specifically, when consonants /l/, /z/, and /n/ are articulated (e.g. frames 12, 27, 39, 52, 65, 79), the relatively rapid tongue tip constrictions used to create these consonants are clearly shown in the area function dynamics (grid line 3). And, when the vowel /ee/ is articulated (frame 31-34 & 117-122), vocalic tongue body constrictions are observable in the palatal region (grid lines 4-7), as is the pharyngeal volume expansion (grid line 12-14) associated with /ee/’s tongue body fronting.
Conclusion
We demonstrate a 3D RT-MRI technique for the study of human speech production that achieves 2.4 x 2.4 x 5.8 mm3 spatial resolution and 72 ms temporal resolution over a 200 x 200 x 70 mm3 FOV. This is achieved by combining a minimum-phase 3D slab excitation, pseudo golden-angle stack-of-spirals, and constrained image reconstruction. This promising tool for speech science for the first time enables a direct comprehensive assessment of vocal tract area function dynamics during speaking.Acknowledgements
This work was supported by NIH Grant R01DC007124 and NSF Grant 1514544. We thank Rachel Walker for helpful discussion and analysis of the 3D data.References
1. Lingala SG, Sutton BP, Miquel ME, Nayak KS. Recommendations for real-time speech MRI. Journal of Magnetic Resonance Imaging. 2016;43(1):28–44.
2. Bresch E, Kim YC, Nayak K, Byrd D, Narayanan S. Seeing speech: Capturing vocal tract shaping using real-time magnetic resonance imaging. IEEE Signal Processing Magazine. 2008;25(3):123–129.
3. Scott AD, Wylezinska M, Birch MJ, Miquel ME. Speech MRI: Morphology and function. Physica Medica. 2014;30(6):604–618.
4. Lingala SG, Zhu Y, Kim Y, Toutios A, Narayanan S, Nayak KS. A fast and flexible MRI system for the study of dynamic vocal tract shaping. Magnetic Resonance in Medicine. 2017;77(1):112-125.
5. Burdumy M, Traser L, Burk F, Richter B, Echternach M, Korvink JG, Hennig J, Zaitsev M. One-second MRI of a three-dimensional vocal tract to measure dynamic articulator modifications. Journal of Magnetic Resonance Imaging. 2017;46(1):94-101.
6. Fu M, Barlaz MS, Holtrop JL, Perry JL, Kuehn DP, Shosted RK, Liang ZP, Sutton BP. High-frame-rate full-vocal-tract 3D dynamic speech imaging. Magnetic Resonance in Medicine. 2017;77(4):1619–1629.
7. Santos JM, Wright G a, Pauly JM. Flexible real-time magnetic resonance imaging framework. Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2004;2:1048–1051.
8. Pauly J, Nishimura D, Macovski A, Roux P Le. Parameter Relations for the Shinnar-Le Roux Selective Excitation Pulse Design Algorithm. IEEE Transactions on Medical Imaging. 1991;10(1):53–65.
9. Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M. Berkeley Advanced Reconstruction Toolbox. In: Proceedings of the International Society of Magnetic Resonance in Medicine, Toronto, Canada. Vol. 23. 2015. p. 2486.
10. Kim J, Kumar N, Lee S, Narayanan S. Enhanced airway-tissue boundary segmentation for real-time magnetic resonance imaging data. Proceedings of the 10th International Seminar on Speech Production (ISSP). 2014:222–225.
11. Skordilis ZI, Toutios A, Toger J, Narayanan S. Estimation of vocal tract area function from volumetric Magnetic Resonance Imaging. IEEE International Conference on Acoustics, Speech and Signal Processing. 2017. p. 924–928.
Figures